MathScinet es una base de datos referencial creada en 1996 por la prestigiosa American Mathematical Society. Versión electrónica de Matemathical Review (MR), en esta base de datos se nos proporcionan reseñas, resúmenes e información bibliográfica sobre literatura científica matemática generada por MR desde su creación en 1940 y también referencias bibliográficas a revistas de matemáticas publicadas desde 1810 y que han sido digitalizadas por diversos proyectos. MathScinet incorpora cada año 125.000 registros clasificados según la Clasificación de Materias de Matemáticas (Mathematics Subject Classification o MSC). Con un total de 3 millones de registros y unos 2 millones de enlaces a artículos originales, es un recurso fundamental para la investigación y estudio de todo lo relacionado con las matemáticas.
El acceso a MathScinet para los miembros de la Universidad Nebrija es muy sencillo. Hay dos opciones desde la página principal del Catálogo-OPAC: buscar MathScinet directamente por su nombre desde la caja de búsqueda del formulario de consulta; o bien pinchar en la pestaña “Recursos Web” y luego hacer clic en “Bases de datos (solo dominio Nebrija)”. Busca entre los resultados MathScinet y clica en acceso a la base de datos. Identifícate con tu cuenta de correo Nebrija y contraseña.
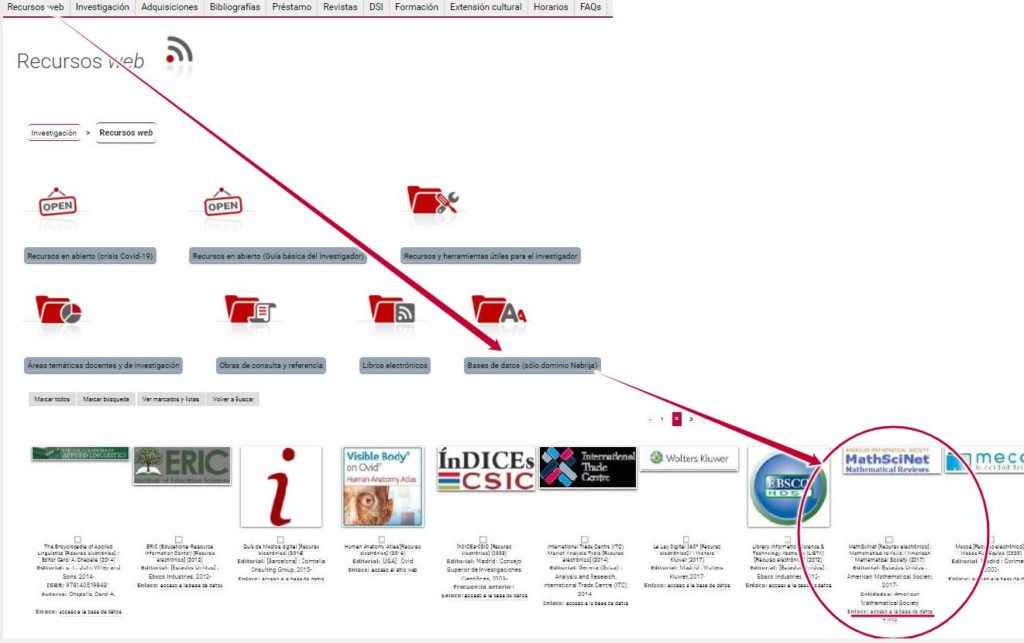
Imagen: Acceso a MathScinet desde el OPAC. Fuente: Biblioteca
La primera pantalla que encontramos cuando accedemos a MathScinet es la “Página principal”, donde podemos elegir hacer la búsqueda en:
- Publicaciones
- Autores
- Revistas
- Citations
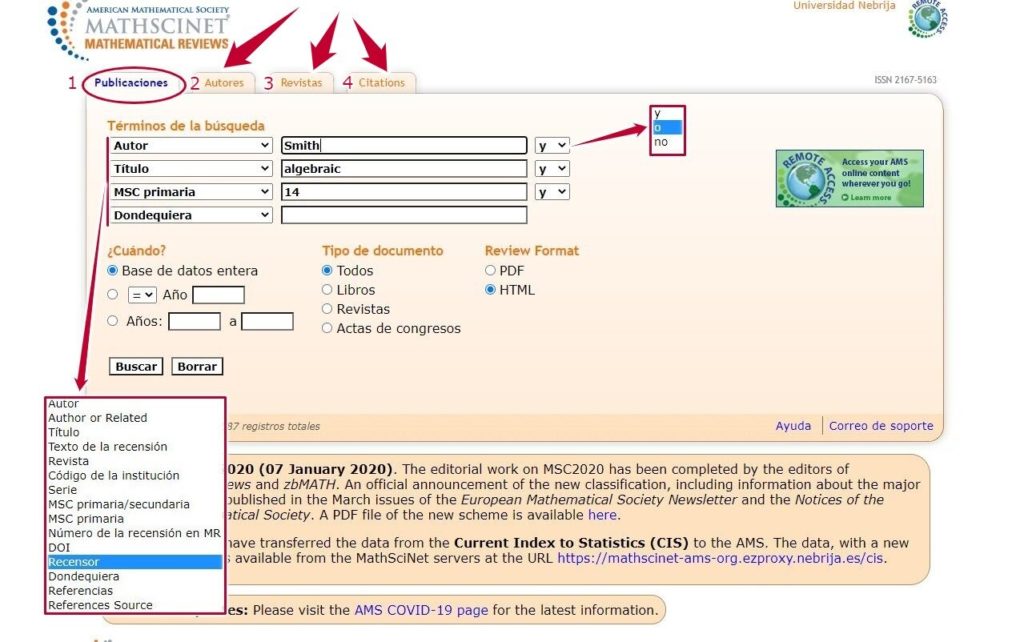
Imagen: Página principal. Fuente: MathScinet
1.Publicaciones
En la pestaña “Publicaciones” tenemos la opción de buscar por diferentes criterios (“Términos de la búsqueda”). Si utilizamos los operadores de búsqueda booleanos (y, o, no) conectaremos de manera lógica los términos por los que lanzaremos la búsqueda y los resultados de esta serán más precisos. Podemos jugar con los operadores booleanos y así, por ejemplo, si solo recordamos dos palabras del título de un artículo que nos interesa, elegiremos la opción “Título” en dos de las cajas de búsqueda y escogemos el operador booleano “Y”. De esta manera nos aproximaremos mucho más a ese título del que solo tenemos una mínima información.
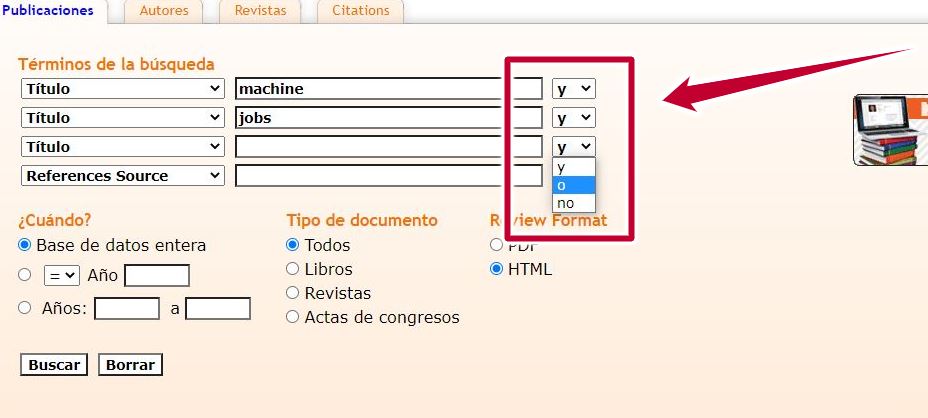
Imagen: Operadores booleanos. Fuente: MathScinet
Pero además de por título, tenemos diferentes opciones para la búsqueda y son las siguientes:
Author: por nombre o apellidos del responsable.
Autor/ related: con esta búsqueda, la base de datos nos encontrará todo lo relacionados con ese autor además de los documentos donde es principal responsable. Por ejemplo, si un autor es también editor o traductor, recuperaremos en los resultados los documentos donde dicho autor ejerza alguno o ambos aspectos.
Título: si conoces el título o alguna palabra del título.
Texto de la recensión: lanzamos la búsqueda sobre los resúmenes de los artículos referenciados. Si la búsqueda que vas hacer es por un conjunto de palabras, por ejemplo “financial mathematics”, no te olvides de las comillas que hacen que esas dos palabras sean buscadas como una.
Revista: por título de la revista (completo, parcial o forma abreviada) o ISSN de la misma.
Series: por el nombre de la serie.
Código de la institución: lanzamos la búsqueda por el código de la institución donde realiza un autor su labor de investigación. Los códigos puedes buscarlos en Math Reviews Institution Codes and Addresses Lookup. Uno de los códigos asignados para la Universidad Nebrija, por ejemplo, es E-NEBR-IEP, que corresponde al Departamento de Ingeniería Industrial Escuela Politécnica Superior de la Universidad Nebrija. Si escribimos este código en la caja de búsqueda con este criterio, MatchScinet nos dará como resultado todo lo que hay en su base de datos con ese código.
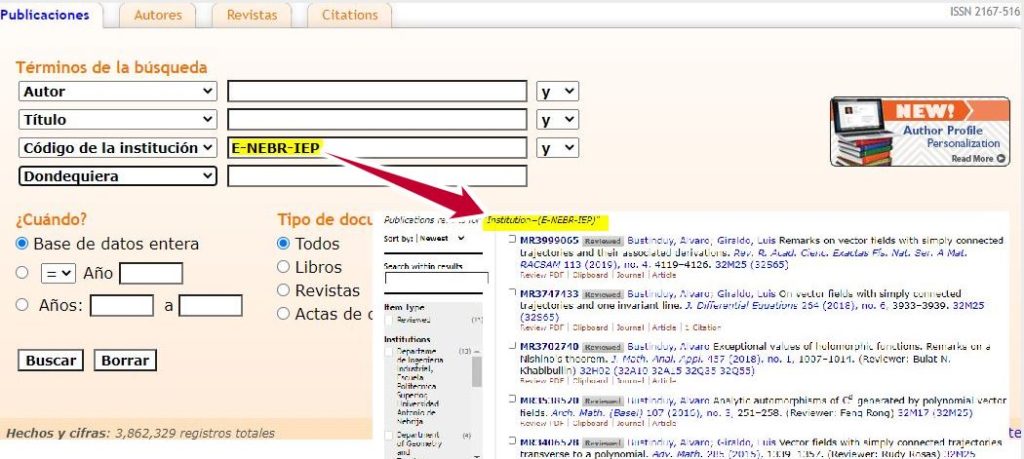
Imagen: Búsqueda y resultado por código de la institución. Fuente: MathScinet
MSC primaria/secundaria y MSC primaria: cada registro de la base de datos tiene, asignado por el editor de la revista donde se ha publicado el artículo, un código según la Mathematics Subject Classifications (MSC). Por ejemplo, si queremos buscar información sobre “teoría de números”, en el MSC el número asignado para esa materia es 11-XX; pero si queremos especificar más y buscar los documentos que traten sobre “teoría de números elemental”, el número que le corresponde a esa materia es el 11Axx. Así, y si buscamos con este último número con las opciones MSC primaria/secundaria o MSC primaria, la base de datos nos proporcionará todos los documentos que hagan referencia a la “teoría de números elemental”.

Imagen: Búsqueda y resultado por MSC. Fuente: MathScinet
Número de la recesión en MR: búsquedas por el número dado por Mathematical Reviews(MR) a cada registro. Consta de las letras MR (que se pueden obviar al buscar) y siete números (si el número comienza con algún cero se puede obviar también). MR4081801, por ejemplo, corresponde a la reseña del artículo títulado “Lotka-Volterra competition model on graphs” de Antonín Slavík.
DOI: el Digital Object Identifier o DOI es el número unívoco que identifica a un objeto digital. Por ejemplo, el DOI del artículo “A software framework to generate two-body potentials using Curvature Constrained Splines” es 10.1016/j.cpc.2020.107602.
Recensor: por el autor/a que ha revisado el artículo y lo ha reseñado.
Dondequiera: lanza la búsqueda de un término en cualquiera de los campos del registro: autor/a, título, revista etc.
Referencias: se realiza una búsqueda por el listado de referencias del registro.
Por último, señalar que podemos acotar nuestras búsquedas por fecha, tipo de documento y formato. Con estas opciones podremos concretar el campo de búsqueda y obtener unos resultados más pertinentes.
2. Autores
En la pestaña “Autores” tenemos la posibilidad de buscar a un autor y acceder un perfil profesional donde veremos las distintas facetas de su trabajo científico: números de citas o publicaciones, en que área matemática ha investigado con más asiduidad o el autor con el que ha colaborado más veces, cuando comenzó su labor investigadora etc. Además, clicando en “Refine Search”, volveremos a la pestaña “Publicaciones”, pero teniendo ya a ese autor como referencia en la búsqueda. Si sabemos el “MR Author ID”, que es un número que identifica a un autor, no puede haber confusión con autores con el mismo o similar nombre porque cada uno tendrá su número (Li, Tie Jun tiene el número 970001; Li, Tiejun el 674248).
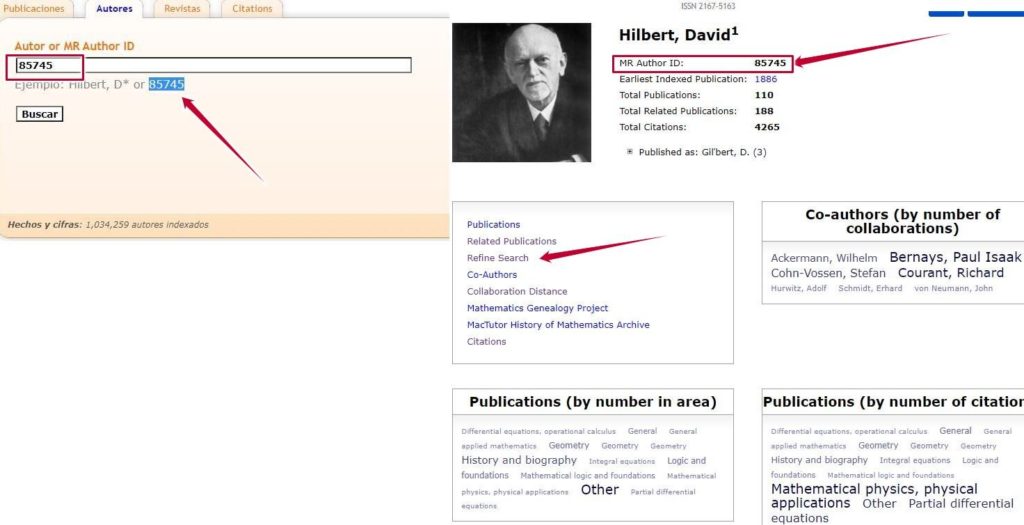
Imagen: Búsqueda por autores. Fuente: MathScinet
3. Revistas
Desde esta pestaña accederemos a las fichas informativas de las revistas y podremos consultar las reseñas que haya de sus artículos en MathScinet y enlazar a su portal web. También se nos ofrece toda la información sobre la revista: datos que la identifican, porcentaje de citas, autores que más han colaborado, temas que más han desarrollado etc.
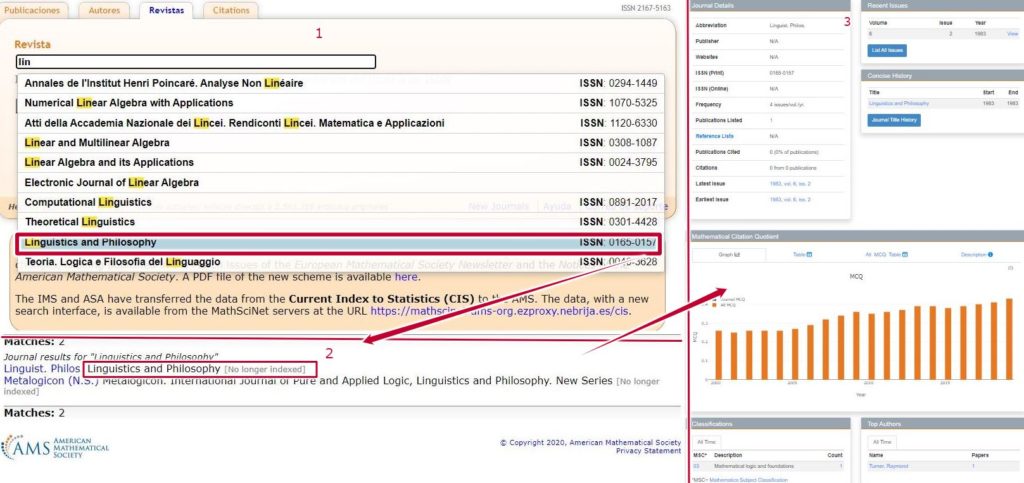
Imagen: Revistas. Fuente: MathScinet
4.Citaciones
En esta pestaña obtendremos información sobre las citaciones que ha tenido un artículo, libro o autor mediante estas opciones de búsqueda:
Citaciones Autores: con esta búsqueda sabremos cuantas veces o por cuantos autores ha sido citado un autor o sus artículos más citados de mayor a menor.
Citaciones Revistas: el resultado de esta búsqueda es el número de citas que ha tenido una revista en un año concreto.
Search by Subject: si buscas por materias recuperas los artículos que más han sido citados según un área temática de la Mathematics Subject Classification (MSC). Por ejemplo, si queremos saber que artículos han sido citados más veces con la materia “Fluid mechanics”, escribiríamos en la caja de búsqueda “76”, que es el número que le corresponde a esa materia en la MSC.
Search by Year: ofrece, de mayor a menor, los artículos o libros escritos en un año en concreto que han sido más veces citados desde su publicación.
Top (10) Lists: recupera los documentos más citados en un año no teniendo en cuenta cuando estén escritos y publicados. El MCQ (Mathematical Citation Quotient) para revistas es el promedio del número de citas que una determinada revista tiene durante cinco años divido por el número de artículos publicados en ese mismo periodo por la revista.
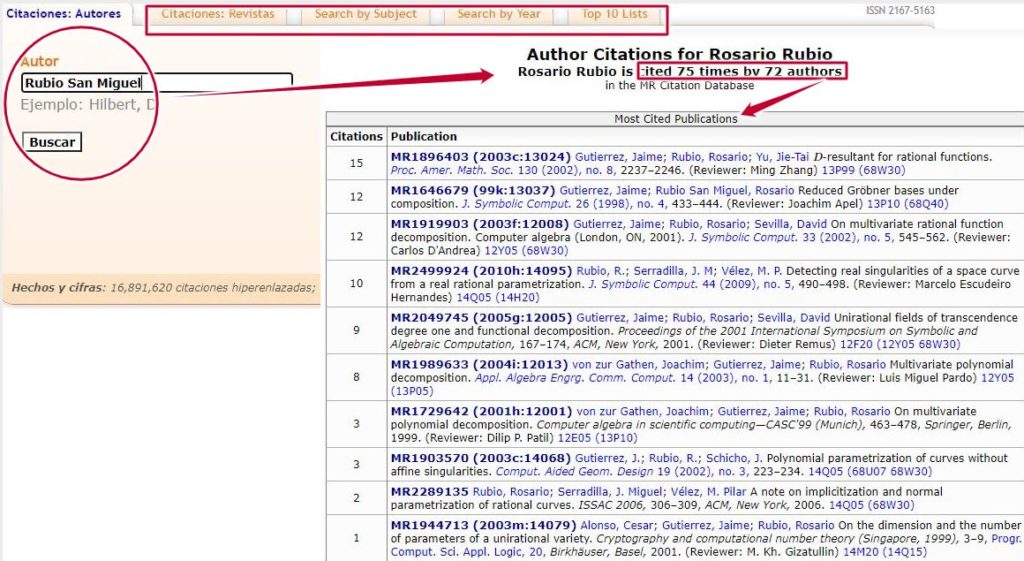
Imagen: Citaciones. Fuente: MathScinet
Una vez realizada la búsqueda, y obtenidos los resultados oportunos, seleccionamos de la lista sugerida un registro y accedemos a la ficha bibliográfica del documento: el nombre del autor o autores, donde se encuentra el artículo y un enlace a la revista que lo publica, que artículos lo han citado, resumen, si el artículo esta revisado o no etc.
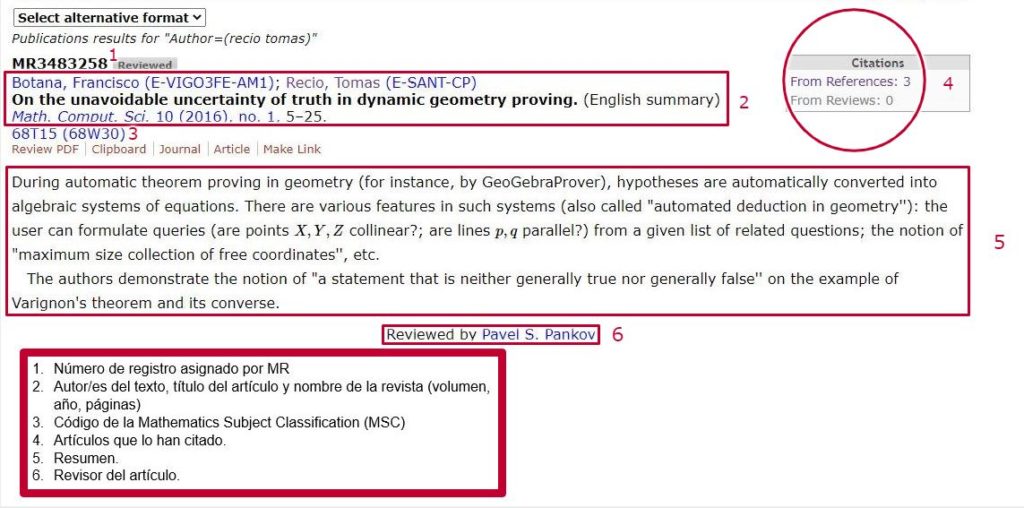
Imagen: Ficha del documento. Fuente: MathScinet
También cabe señalar que MathScinet, además de las opciones de búsqueda reseñadas ya en este texto, permite también otro tipo de búsquedas más específicas y hechas ex profeso para esta base de datos. Estas las encontramos en la sección que se denomina “Nuevas herramientas”.

Imagen: Nuevas herramientas. Fuente: MathScinet
Las opciones que nos encontramos en esta sección son:
Búsqueda en MSC: podremos servirnos de esta búsqueda como guía para la consulta por un tema en concreto con los criterios MSC primaria/secundaria y MSC primaria en la pestaña publicaciones.
Distancia entre colaboradores: Paul Erdős fue uno de los autores más prolíficos en el campo de las matemáticas y el número Erdős mide la distancia colaborativa de un autor respecto a Erdős. Con este indicador bibliométrico de Mathscinet sabremos el grado de colaboración de un autor con Paul Erdős o la distancia colaborativa entre dos autores.
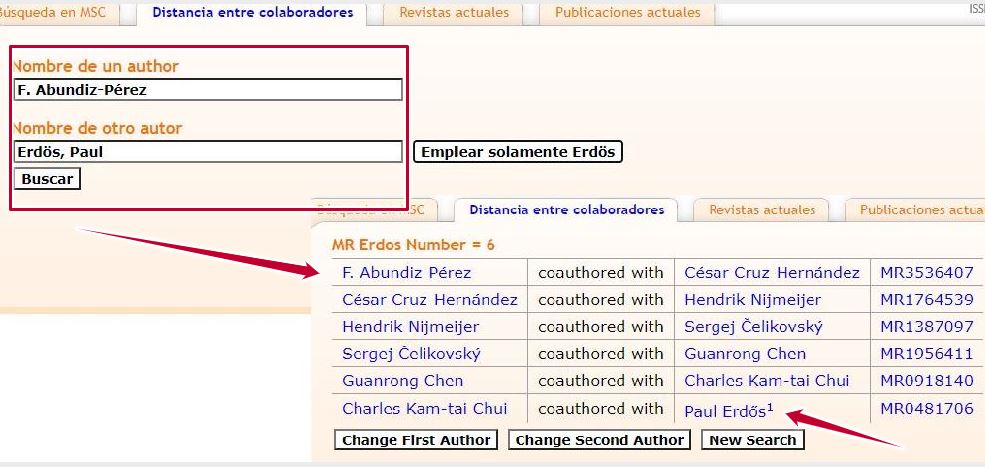
Imagen: Distancia entre colaboradores. Fuente: MathScinet
Revistas actuales: nos muestra y permite saber las revistas que han sido indizadas durante un determinado periodo de tiempo.
Publicaciones actuales: si queremos saber que se ha publicado en los últimos seis meses. Las opciones que nos ofrecen al hacer la búsqueda son con recensiones o solo indexadas, de una materia de MSC determinada o de un tipo de documento concreto.
Hasta aquí las múltiples posibilidades que MatchScinet contempla para sacar el mejor provecho de los recursos de los que dispone. No obstante, y si queremos profundizar más en su uso, en la misma página tenemos tutoriales o un blog, a cuyo acceso tenemos permiso, y en el que encontraremos entradas sobre las novedades que de MathScinet van surgiendo. También nos facilitan nuestro trabajo con la sección “Portapapeles”, donde podremos ir guardando los artículos que nos pueden interesar durante la búsqueda (solo tienes que pinchar cuando estés en la ficha del artículo a “clipboard”).

Imagen: Portapapeles y tutoriales. Fuente: MathScinet
En conclusión, MatchScinet es un recurso muy útil en el campo de las matemáticas y el estudio de áreas relacionadas con esta ciencia (informática, ingeniería, física, estadística, etc.) y que va ayudarte de manera notable en tus trabajos, estudios o investigaciones. Una herramienta para estudiantes e investigadores de la Universidad Nebrija, de uso intuitivo y sencillo, y que te servirá como brújula y punto de apoyo para indagar y estar informado sobre las publicaciones académicas más relevantes y actuales del universo matemático.
José Luis Salado
Servicio de Biblioteca
